(1) Číselné soustavy

image_pdfimage_print

Číselné soustavy

Osnova

 

  1. Poziční číselné soustavy
    1. dvojková
    2. převod (substituční metota, Eurelův alg)
  2. Nepoziční číselné soustavy
    1. římské číslice
      1. základní symboly
      2. původ symbolů
      3. nula
      4. dnešní užití
      5. IIII nebo IV
      6. MS Excel & římská čísla

 

  • způsob reprezentace čísel.
  • podle způsobu určení hodnoty čísla z dané reprezentace rozlišujeme dva hlavní druhy číselných soustav:
    • A) poziční číselné soustavy
    • B) nepoziční číselné soustavy.

A) Poziční číselné soustavy

  • charakterizovány tzv. základem neboli bází (anglicky radix, značí se r),
    • = kladné celé číslo definující maximální počet číslic, které jsou v dané soustavě k dispozici.
  • Poziční soustavy (kromě jedničkové) se nazývají také polyadické (= vlastnost, že číslo v nich zapsané lze vyjádřit součtem mocnin základu dané soustavy vynásobených příslušnými platnými číslicemi)

Mezi nejčastěji používané poziční číselné soustavy patří:

  • jedničková — unární, r=1
    • přestože si to ani neuvědomujeme, tuto soustavu běžně používáme při počítání na prstech nebo při psaní čárek označujících počet piv na účet v restauračních zařízeních. Může být řazena mezi speciální poziční soustavy nebo i zcela mimo dělení na poziční/nepoziční soustavy.
  • dvojková (BIN) — binární, r=2
    • přímá implementace v digitálních elektronických obvodech (použitím logických členů), čili interně ji používají všechny moderní počítače
  • osmičková (OCT) — oktální, oktalová, r=8
  • desítková (DEC) — decimální, dekadická, r=10
    • nejpoužívanější v běžném životě
  • dvanáctková — r=12
    • dnes málo používaná, ale dodnes z ní zbyly názvy prvních dvou řádů – tucet a veletucet
  • šestnáctková (HEX) — hexadecimální, r=16
    • používá se v oblasti informatiky, pro číslice 10 až 15 se používají písmena A až F
  • šedesátková — r=60
    • používá se k měření času pro zlomky hodiny; číslice se obvykle zapisují desítkovou soustavou jako 00 až 59 a řády se oddělují dvojtečkou; staré názvy prvních dvou řádů jsou kopa a velekopa.

Každé číslo vyjádřené v poziční soustavě (kromě jedničkové) může mít část celočíselnou a část zlomkovou (např. u desítkové soustavy desetinnou část). Tyto části jsou odděleny znakem, nazývaným desetinnou čárkou (přestože obecně nejde o desetiny). V anglosaských zemích je místo desetinné čárky užívána desetinná tečka.

Dvojková

= číselná soustava, která používá pouze dva symboly: 0 a 1.

  • poziční číselná soustava mocnin čísla 2.
  • Používá se ve všech moderních digitálních počítačích, neboť její dva symboly (0 a 1) odpovídají dvěma jednoduše rozdělitelným stavům elektrického obvodu
    • vypnuto × zapnuto
    • nepravda × pravda
  • Číslo zapsané v dvojkové soustavě se nazývá binární číslo.

Převod

Metoda substituční

  • Substituční metoda slouží k převodu mezi číselnými soustavami. Metoda spočívá v rozepsání převáděného čísla na polynom a následně jeho vyčíslení v cílové soustavě.

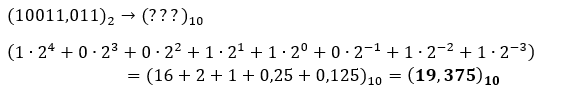
metoda_substituce

Eulerův algoritmus

  • dále

B) Nepoziční číselné soustavy

  • způsob reprezentace čísel, ve kterém není hodnota číslice dána jejím umístěním v dané sekvenci číslic. Tyto způsoby zápisu čísel se dnes již téměř nepoužívají a jsou považovány za zastaralé
  • A=1, B=10, C=100, D=1000, pak by vyjádřením čísla 3542 mohl být například řetězec „AABBBBCCCCCDDD“, ale stejně dobře i „ACDABBCCCCDDBB“ apod. (z hlediska hodnoty, ale za cenu horší srozumitelnosti).

Nevýhody

  • Často neobsahovaly symbol pro nulu a záporná čísla
  • Dlouhý zápis čísel, která výrazně převyšují hodnotu největšího symbolu soustavy

Příklady nepozičních číselných soustav

  • Římské číslice (I, II, III, IV, V)
  • Egyptské číslice
  • Řecké číslice — zápisu čísel pomocí písmen alfabety

Římské číslice

způsob zápisu čísel pomocí písmen abecedy

dnes tento způsob zápisu výjimečný (použití viz dále)

Základní symboly

Římské
číslo		 Arabské
číslo
I 1
V 5
X 10
L 50
C 100
D 500
M 1000

 

  • Často mnemotechnické pomůcky: Ivan Vedl Xénii Lesní Cestou Do Města

Původ symbolů

I

  • Římská čísla vznikla přirozenou cestou. Římané počítali na prstech. Čísla jako 1, 2 a 3 a jím odpovídající znaky I, II a III graficky vyjadřují jednotlivé prsty.

V a X

  • Také tato dvě římská čísla mají svůj původ v lidské ruce:
  • Římská číslice V (5) je vyjádřením dlaně s pěti prsty – V tvoří tvar mezi palcem a malíčkem.
  • Římská číslice X (10) jsou dvě dlaně u sebe (10 prstů).

L a C

  • Latinsky sto je centum – odtud C. Padesát je polovina ze stovky. L tedy vzniklo „rozpůlením“ znaku pro 100 (C).

D a M

  • Tisíc je latinsky mille (odtud M pro 1000). Znak D pro 500 vznikl opět grafickým „půlením“ znaku M, tentokrát svisle. Vznikl tak znak podobný písmenu D.

Nula

  • Číslice nula nemá obecně svůj symbol, přestože Římané číslici 0 a její význam dobře znali.
    • ⇒ hlavní důvod, proč nebyl systém římských číslic přijat za poziční č.s. a byl postupně nahrazován arabskými číslicemi

 

Použití římských číslic dnes

  • díly čí série knih či filmů (v tomto významu jsou vytlačovány arabskými číslicemi)
  • ročníky časopisů či novin (v tomto významu jsou vytlačovány arabskými číslicemi)
  • kapitoly v knihách či článcích (v tomto významu jsou vytlačovány arabskými číslicemi)
  • opakované společenské, sportovní a jiné události (soutěže, závody, přehlídky, sjezdy a slety, války, festivaly, veletrhy, výstavy apod.), ve většině případů však již v praxi začínají převládat arabské číslice
  • rok (prakticky jen na historických nápisech, v moderních textech se používají výhradně arabské číslice)
  • století (v tomto významu jsou vytlačovány arabskými číslicemi)
  • měsíce v roce (v tomto významu jsou vytlačovány arabskými číslicemi)
  • pořadové číslo čtvrtletí (používají se ale i arabské číslice)
  • pro číslice na hodinovém ciferníku
  • pořadová čísla panovníků (např. Karel IV.), pro tento účel se stále používají takřka výhradně římské číslice
  • čísla místních částí obce – v minulosti tvořilo římské číslo místní části dvojici s číslem popisným, nyní se místo něj běžně používá název místní části; označení čtvrtí římskými čísly přežívá jen v některých městech, například Děčíně, částečně v Pardubicích či Mladé Boleslavi atd.
  • třídy silnic (I, II, III) – např. „silnice I. třídy“, „silnice II/201“,
  • souběžné ulice, které jinak mají stejný název (pouze v některých místech, kde bylo názvosloví inspirováno americkými systémy, například na pražském Spořilově)
  • díly či části obcí či katastrálních území či obce, které by jinak měly stejný název, pokud nejsou rozlišeny slovním přívlastkem
  • v českých právních předpisech se podle aktuálních legislativních pravidel vlády římskými čísly bez tečky označují varianty návrhů, čísla článků v novelách předpisů a hlavy (celek nižší než část a vyšší než díl).

V polštině se římské číslice používají takřka výhradně při uvádění století (např. 19. století je XIX wiek).

 IIII nebo IV

  • Hodinové ciferníky se popisují římskými číslicemi. Obvykle používají symbol IIII pro 4 a IX pro 9. Jednou se tak odečítací pravidlo neaplikuje a podruhé ano. Proč? Nabízí se několik vysvětlení:
    • Čtyřznakové IIII vytváří vizuální symetrii s VIII na druhé straně ciferníku, zatímco IV ne
    • IV jsou první dvě písmena jména boha Jupitera (IVPITER)

Microsoft Excel a římská čísla

Funkce:

  • =ROMAN(arabské číslo; forma zápisu) /viz soubor/
  • =ARABIC(římské číslo) (*od verze 2013 resp. 2016 pro MacOS)

Euklidův algoritmus

eul.alg

1-Číselné-soustavy-příklady (1)

Odkazy: